一、PCA简介
主成分分析(PCA)是一种常见的,也是最简单的降维手段,在机器学习中可用于特征提取。即便有时收集到的样本维数很高(即含有过多特征),但与学习任务相关的可能只是某个低维分布,这时就需要有效降维,在缓解维数灾难的同时令得到的低维嵌入仍能很好地描述原样本空间。
二、PCA推导
首先进行任务描述。
设样本 $X∈R^{n \times d}$ , 低维表示$Z∈R^{n \times l} (l<d)$ 。$Z=X \times W$。可以将这个变换看作坐标变换,那么$W$就是$l$个正交基向量(列向量)组成的矩阵,$W^TW=I$。也就是说,我们有n个d维的原样本x,经坐标变换后得到n个$l$维的新样本z。在新坐标系中,$Z$的每一行(即每个新样本)都可看作是原样本在$w_i$方向上的投影。为了更直观地进行坐标变换,我们将样本进行中心化,每个样本都减去均值,使得样本中心落在原点,$\sum_i{x_i=0}$。
我们知道投影可以用内积的形式表示,用$x_iw_1$表示$x_i$(行向量)在$w_1$上的投影长度(还要除以$w_1$的模,这里为基向量,模长为1)。在信号处理中,认为信号的方差较大,噪声方差较小,这个理论可以推广到我们的问题中,也就是希望投影后的样本点比较分散(方差大),如下图(网图侵删):
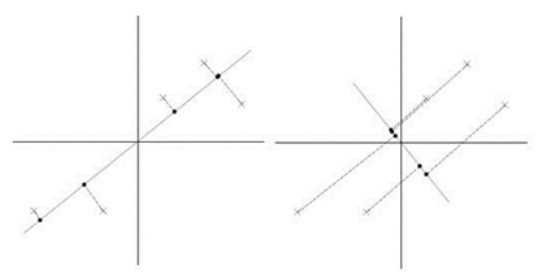
认为第一个投影方向更好,它使得样本投影方差最大。由于样本已中心化,因此方差可用投影长度的均方来表示:
上式取极大就是PCA目标函数的一种形式,利用的是最大方差准则(也可以用最小二乘等准则)。其中$w_1$是要求的第一个投影方向(主方向,对应着W的某一列)。$x_iw_1$是一个标量,它的转置等于本身,目标函数可写成如下形式:
(注:这种方式是机器学习中常用的一种变换,将向量乘积根据需要灵活地结合成矩阵或标量,引入一些可解释性)
显然中间部分就是协方差矩阵($x_i$是行向量)。为了更形式化地表示,直接用$X$代替,并加上之前说的正交基假设,写出完整的目标函数:
是一个约束最优化问题,可引入拉格朗日乘子求解。这里补充一句,我们的目标函数包含一个标准二次型,之所以有最优解是因为它是半正定的(协方差矩阵是半正定矩阵)。目标函数中的$\frac{1}{n}$对结果无影响,在计算时不考虑。引入拉格朗日乘子λ:
对参数求偏导得:
可以看出,为了求目标函数极大,拉格朗日乘子$\lambda$就是协方差矩阵的特征值,我们要求的投影方向向量$w_1$是该特征值对应的特征向量。上面等式两边同时乘$w_1^T$得:
得到的式子左边就是我们的目标函数,那么目标函数可转换为
至此,我们将求最大投影方差问题转换成了求协方差矩阵最大特征值的问题。上面是用一个投影向量$w_1$为例,为了求得d个投影向量组成的变换矩阵W,只需求最大d个特征值对应的特征向量即可。
得到了$W$以后,我们就可以对样本进行降维处理得到$Z:Z=XW$。
三、总结
上面经过严格的目标函数推导,我们得出了主成分分析的求解方法。可以看出这个结果非常“巧合”地映射到了协方差矩阵的特征向量上,使得这个过程有了可解释性。
因为$l<d$,很显然这是一个有损变换。从任务角度来说,我们在特征提取时舍弃了$d-l$个特征,造成了信息丢失。为了减少损失,在降维过程中应尽量舍弃那些用处不大的特征。

