贝叶斯决策的过程

最小风险决策

最小风险决策是贝叶斯决策的一般形式。引入决策代价loss：$\lambda_{ij}=\lambda (\alpha_i|\omega_j)$ ，表示原本属于类 $j$，被错分为类 $i$ 所产生的风险（BTW，$\lambda_{ij}$ 与 $\lambda_{ji}$ 并不相等，有时相差很大。比如肿瘤检测时)。则条件风险 $R(\alpha_i|x) = \sum_{j=1}^{c}\lambda(\alpha_i|\omega_j)P(\omega_j|x)$ 贝叶斯决策就要选择最小化该条件风险的类别 $i$。

当 $\lambda$ 为0/1损失时，$R(\alpha_i|x) = 1 - P(\omega_i|x)$，最小风险决策退化为最小错误率决策，或最大后验决策。

带拒识的决策

在很多模式识别应用中，当最大后验也不是很高，也就是置信度低的情况下，很可能出现了不可分情况，可让分类器拒绝分类。设计拒识风险 $\lambda_r$，表示为：

​

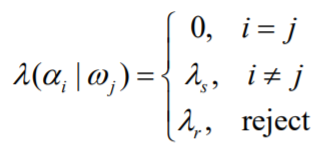
则风险$R$表示为：

​

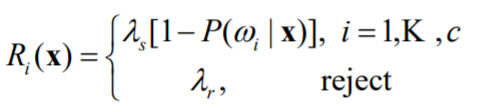
可知当$\lambda_s[1 - P(\omega_i|x)] > \lambda_r$时选择拒识，决策方式写作：

​

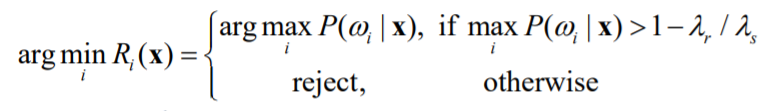
这种写法比较形式化，可以简单的理解$\max P(\omega_i|x)$小于某个阈值时视为置信度过低，拒绝分类。

贝叶斯决策具体过程

前面定义了贝叶斯决策的风险函数，主要与类别后验相关。根据贝叶斯公式$P(\omega_i|x) = \frac{P(x|\omega_i)P(\omega_i)}{P(x)}$，给出贝叶斯决策的几种判别函数：

​ $g_i(x) = P(\omega_i|x)$ ，$g_i(x) = P(x|\omega_i)P(\omega_i)$，$g_i(x) = -R(\alpha_i|x)$

还有一种常用的似然形式：$g_i(x) = \log P(x|\omega_i) + \log P(\omega_i)$

则判别决策为$\arg\max g_i(x) $。令判别函数相等可得到决策面，能够在几何上对特征空间进行分割，让我们对分类有直观的认识，加深对分类器的理解。

贝叶斯决策几个关键步骤：

1、估计类条件概率密度$P(x|\omega_i)$

2、估计类先验概率$P(\omega_i)$ (一般从训练数据中统计)

3、决策代价$\lambda_{ij}$。（除非面向特定应用，否则一般用0/1损失，即最大后验决策）

类条件概率密度估计方法

1、参数法。假定概率密度函数形式，如高斯分布。

2、非参数法。如Parzen窗，k-NN。

3、半参数法。高斯混合。

高斯密度函数法

假定类条件概率密度符合高斯分布，那么只要估计出均值和协方差矩阵即可得到$p(x|\omega_i)$。参数估计过程详见最大似然和贝叶斯参数估计。

将条件概率分布写成多元高斯形式:

​

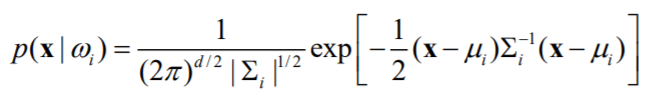
得到似然形式的判别函数$g_i(x)$：

​

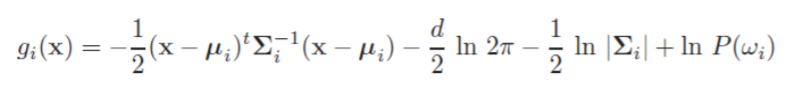
在数据的不同分布情况下，我们能得到一些特殊的形式。下面根据协方差矩阵的3种形式（逐渐推广），直观地来看一下数据分布、先验等对贝叶斯决策的影响。

• Case 1 $\Sigma_i =\sigma^2$

  协方差矩阵是对角矩阵，且对角元素相等。这种情况说明数据在各个维度（或说特征，对应特征空间）上的分布独立，且各个维度的方差均为$\sigma^2$。从几何上来说，所有类的样本分别落在一个形状相同的超球体当中。判别函数用于分类，因此只考虑类别相关的部分，即与i相关的项，其余部分不考虑，判别函数写成：

  

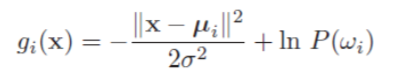
  将二范数平方展开，得到

  

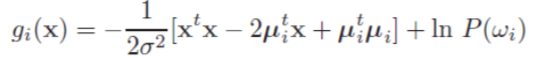
  注意到$x^tx$与类别无关，可不考虑。为了直观地获得一般形式的决策超平面，我们将判别函数写成线性形式：

  

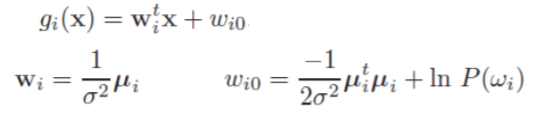
  以二分类情况为例，令$g_i(x)-g_j(x)=0$即可得到决策面，表示为：

  
  

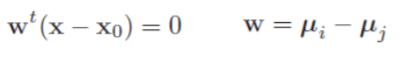
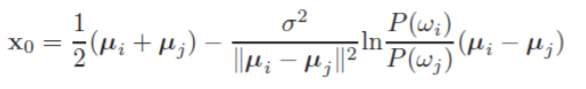
  我们观察到，法向量等于两类类心点的差，因此决策面与两个中心点连线垂直。决策面与这条直线相交于点$x_0$。

  再来观察$x_0$，当先验概率相等即$P(\omega_i)=P(\omega_j)$时，$x_0$第二项为0，那么该点落在两中心点连线的中心，如图（图来自《模式分类第二版》）

  

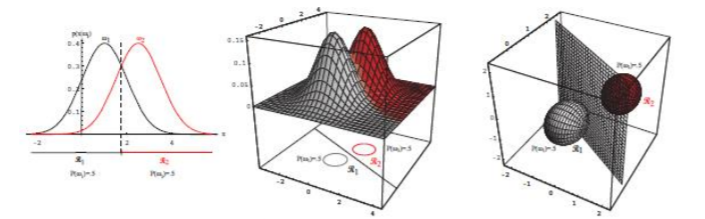
  当先验不相等时，决策面将随着点$x_0$向先验概率小的方向偏移，如下图

  

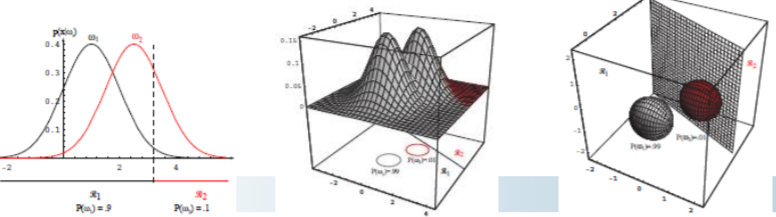
  这里给出的是比较极端的一种情况，先验相差较大，$P(\omega_1)=0.9,P(\omega_2)=0.1$。这就使得决策面偏移很大，甚至没有落在两个均值向量之间，可见先验概率对分类结果也有很大的影响。当然，当$\sigma^2$远小于$||\mu_i-\mu_j||^2$时，$x_0$第二项将变得很小，使决策面对先验不再敏感。

• Case 2 $\Sigma_i =\Sigma$

  各个类的协方差矩阵相同，但均值各不相同。这显然是Case 1的一个推广。

  首先同样只保留类别相关项，即

  ​

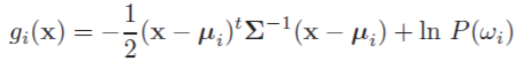
  将判别函数按照与刚才同样的方法转换成一般形：

  ​
  ​

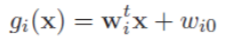
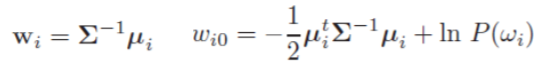
  再得到决策面：

  ​

  ​

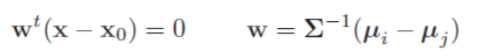
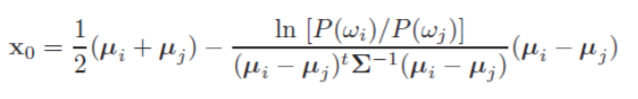
  我们再来看这种形式。首先，法向量经一个矩阵变换，使得决策面不再垂直于两中心点连线，但仍与直线交于点$x_0$。当先验概率相等时，$x_0$位于连线中点，否则依然偏向先验小的一类。如下图所示。

  ​

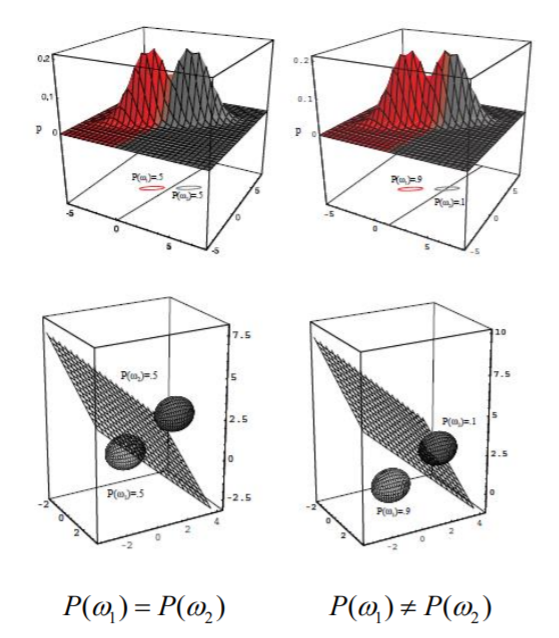
  由于协方差矩阵不再是对角矩阵，各个维度相互依赖，使得样本分布的形状呈椭球形，而不再是标准的球形。但由于各类协方差矩阵相同，因此它们的分布形状都是一样的。可以观察一下，决策面的方向其实与椭球最长轴的方向一致，这与协方差矩阵的几何性质有关，主成分分析（PCA）也利用了这一点。

• Case 3 $\Sigma_i$任意

  这是最一般的情况，各个类的样本分布形状各不相同，由贝叶斯判别边界求出的决策面也不再是超平面，而成为了超曲面。

  《模式分类第二版》里给出了几个直观的2D情况的例子：

  ​

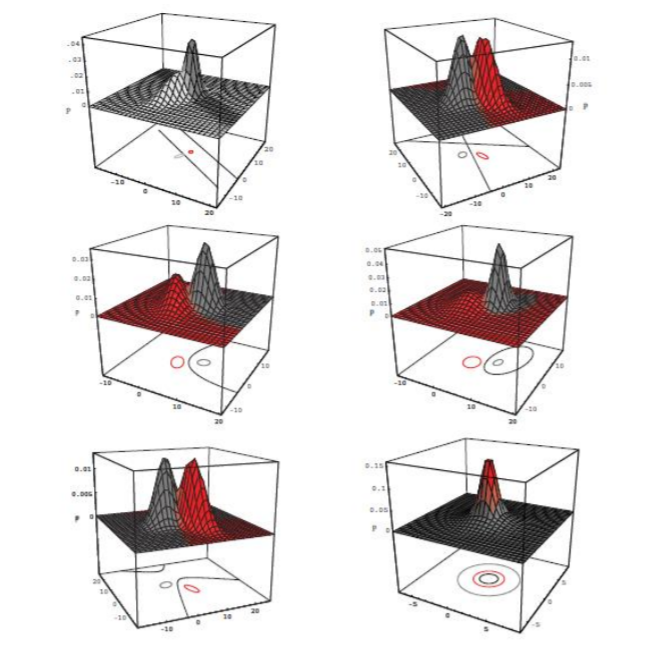
  总结一下，列出这三种情况其实就是为了说明数据分布情况对高斯情况下决策的影响。这些图也帮助我们理解了协方差矩阵是如何反映数据分布的。

分类错误率

考虑二分类，决策面把特征空间分成$R_1$和$R_2$两个部分，那么错误分类的情况发生在真实类为$\omega_1$，观测值落在R2中，或真实类为$\omega_2$，观测值落在$R_1$中时。形式化表示为：

​

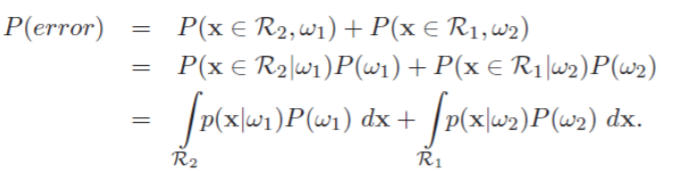
推广到一般形式，计算正确率更为方便：

​

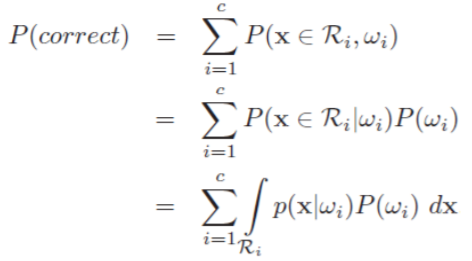
再来考虑最大后验概率决策，即0/1损失的情况：

​

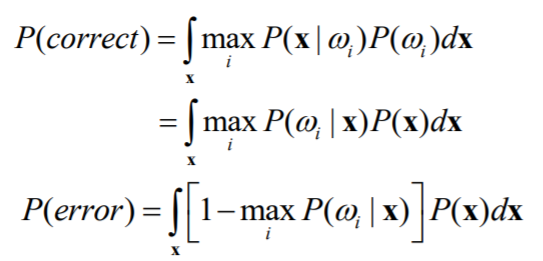
总结

贝叶斯分类器使用的是最小错误率决策，理论情况下，即条件概率密度函数和风险$\lambda$被正确估计时是最优分类器。然而通常我们都仅仅是假设了条件概率密度函数的形式，如前面所述的高斯分布，导致效果出现偏差。事实上这里有两层误差，一个是结构误差，即对真实样本分布的错误估计，另一个是模型参数估计误差。这两层误差是造成贝叶斯分类器效果不好的原因，而并非分类器本身的缺陷。